Optical scalars

In general relativity, optical scalars are a set of scalars that describe various properties of null geodesic congruences. The three optical scalars used in general relativity are expansion, shear and twist (vorticity) and were first defined and used by Sachs (1961). Given a vector field $k$ tangent to the null geodesic, the optical scalars are defined as follows.

Expansion

The expansion of the null ray is defined as

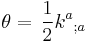
$\theta = \, \frac{1}{2} k^a{}_{;a}$

Shear

The shear of the null ray is defined as

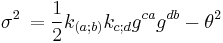
$\sigma ^2 \, = \frac{1}{2}k_{(a;b)}k_{c;d}g^{ca}g^{db} - \theta ^2$

Twist

The twist of the null ray is defined as

$\omega ^2 \, = k_{[a;b]}k_{c;d}g^{ca}g^{db}$